P2: Punto simétrico de P1 respecto de la recta r

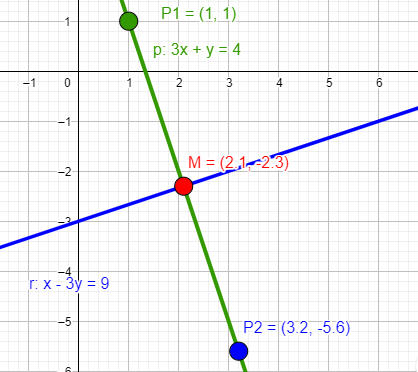
Dada la recta r: x-3y=9, vamos a calcular el punto simétrico de P1 (1,1) respecto de esa recta. Pasos:

1. Calcular la pendiente de r --> m=1/3
2. Calcular la pendiente perpendicular a m --> m´=3
3. Calcular la recta perpendicular a r que pasa por P1 --> y-1=3(x-1)
4. A esta recta la vamos a llamar p --> 3x+y=4
5. Calcular la intersección entre las dos rectas r y p --> M
6. Como M es el punto medio entre P1 y P2 se cumplirá que P2 = 2M-P1
7. Así obtenemos P2 que es el punto simétrico de P1 respecto de la recta r